Viscosity-Storage-Dominated Penny Shaped Hydraulic Fracture

Context

In this example, we simulate the propagation of a radial hydraulic fracture in viscosity-storage-dominated regime, another classic benchmark in hydraulic fracturing (Settgast et al., 2016). The fracture develops as a planar fracture with an elliptical cross-section perpendicular to the fracture plane and a circular fracture tip. Unlike the toughness-storage-dominated fractures, fluid frictional loss during the transport of viscous fracturing fluids governs the growth of viscosity-storage-dominated fractures. We solve this problem using the hydrofracture solver in GEOS. We simulate the change in length, aperture, and pressure of the fracture, and compare them against the corresponding analytical solutions (Savitski and Detournay, 2002).

Input file

This example uses no external input files. Everything we need is contained within two GEOS input files:

inputFiles/hydraulicFracturing/pennyShapedViscosityDominated_base.xml

inputFiles/hydraulicFracturing/pennyShapedViscosityDominated_benchmark.xml

Python scripts for post-processing and visualizing the simulation results are also prepared:

inputFiles/hydraulicFracturing/scripts/hydrofractureQueries.py

inputFiles/hydraulicFracturing/scripts/hydrofractureFigure.py

Description of the case

We model a radial fracture emerging from a point source and forming a perfect circular shape in an infinite, isotropic, and homogenous elastic domain. As with the viscosity-dominated KGD problem, we restrict the model to a radial fracture developed in a viscosity-storage-dominated propagation regime. For viscosity-dominated fractures, more energy is applied to move the fracturing fluid than to split the intact rock. If we neglect fluid leak-off, the storage-dominated propagation occurs from most of the injected fluid confined within the opened surfaces. We use a low rock toughness ( $0.3 MPa { \sqrt{m} }$ ), and the slickwater we inject has a constant viscosity value ( $1.0 cp$ ) and zero compressibility. In addition, we assume that the fracture surfaces are impermeable, thus eliminating fluid leak-off. With this configuration, our GEOS simulations meet the requirements of the viscosity-storage-dominated assumptions.

The fluid injected in the fracture follows the lubrication equation resulting from mass conservation and Poiseuille’s law. The fracture propagates by creating new surfaces if the stress intensity factor exceeds the local rock toughness $K_{IC}$ . By symmetry, the simulation is reduced to a quarter-scale to save computational cost. For verification purposes, a plane strain deformation is considered in the numerical model.

We set up and solve a hydraulic fracture model to obtain the evolution with time of the fracture radius $R$ , the net pressure $p_0$ and the fracture aperture $w_0$ at the injection point for the penny-shaped fracture developed in viscosity-storage-dominated regime. Savitski and Detournay (2002) presented the corresponding asymptotic solutions, used here to validate the results of our GEOS simulations:

$R(t) = 0.6955 (\frac{ E_p Q_0^3 t^4 }{ M_p })^{ 1/9 }$

$w_0(t) = 1.1977 (\frac{ M_p^2 Q_0^3 t }{ E_p^2 })^{ 1/9 }$

$p_0( \Pi, t ) = {\Pi}_{mo} (\xi) (\frac{ E_p^2 M_p }{ t })^{ 1/3 }$

where the plane modulus $E_p$ is related to Young’s modulus $E$ and Poisson’s ratio $\nu$ :

$E_p = \frac{ E }{ 1-\nu^2 }$

The term $M_p$ is proportional to the fluid viscosity $\mu$ :

$M_p = 12 \mu$

The viscosity scaling function ${\Pi}_{mo}$ is given as:

${\Pi}_{mo} (\xi) = A_1 [ 2.479 - \frac{ 2 }{ 3 ( 1 - \xi )^{ 1/3 } } ] - B [ \text{ln}(\frac{ \xi }{ 2 }) + 1]$

with $A_1 = 0.3581$ , $B = 0.09269$ , $c_1 = 0.6846$ , $c_2 = 0.07098$ , and $\xi = r/R(t)$ denoting a dimensionless radial coordinate along the fracture.

For this example, we focus on the Mesh, the Constitutive, and the FieldSpecifications tags.

Mesh

The following figure shows the mesh used in this problem.

We use the internal mesh generator to create a computational domain ( $400\, m \, \times 400 \, m \, \times 800 \, m$ ), as parametrized in the InternalMesh XML tag. The structured mesh contains 80 x 80 x 60 eight-node brick elements in the x, y, and z directions respectively. Such eight-node hexahedral elements are defined as C3D8 elementTypes, and their collection forms a mesh with one group of cell blocks named here cb1. Local refinement is performed for the elements in the vicinity of the fracture plane.

Note that the domain size in the direction perpendicular to the fracture plane, i.e. z-axis, must be at least ten times of the final fracture radius to minimize possible boundary effects.

  <Mesh>
    <InternalMesh
      name="mesh1"
      elementTypes="{ C3D8 }"
      xCoords="{ 0, 100, 200, 400 }"
      yCoords="{ 0, 100, 200, 400 }"
      zCoords="{ -400, -100, -20, 20, 100, 400 }"
      nx="{ 50, 10, 20 }"
      ny="{ 50, 10, 20 }"
      nz="{ 10, 10, 20, 10, 10 }"
      cellBlockNames="{ cb1 }"/>
  </Mesh>

The fracture plane is defined by a nodeset occupying a small region within the computation domain, where the fracture tends to open and propagate upon fluid injection:

    <Box
      name="core"
      xMin="{ -500.1, -500.1, -0.1 }"
      xMax="{ 500.1, 500.1, 0.1 }"/>

Solid mechanics solver

GEOS is a multi-physics platform. Different combinations of physics solvers available in the code can be applied in different regions of the domain and be functional at different stages of the simulation. The Solvers tag in the XML file is used to list and parameterize these solvers.

Three elementary solvers are combined in the solver Hydrofracture to model the coupling between fluid flow within the fracture, rock deformation, fracture deformation and propagation:

    <Hydrofracture
      name="hydrofracture"
      solidSolverName="lagsolve"
      flowSolverName="SinglePhaseFlow"
      surfaceGeneratorName="SurfaceGen"
      logLevel="1"
      targetRegions="{ Fracture }"
      maxNumResolves="1"
      initialDt="0.1">
      <NonlinearSolverParameters
        newtonTol="1.0e-4"
        newtonMaxIter="10"
        maxTimeStepCuts="5"
        logLevel="1"/>
      <LinearSolverParameters
        solverType="gmres"
        preconditionerType="mgr"
        logLevel="1"
        krylovAdaptiveTol="1"/>
    </Hydrofracture>

Rock and fracture deformation are modeled by the solid mechanics solver SolidMechanicsLagrangianSSLE. In this solver, we define targetRegions that includes both the continuum region and the fracture region. The name of the contact constitutive behavior is specified in this solver by the contactRelationName.

    <SolidMechanicsLagrangianSSLE
      name="lagsolve"
      timeIntegrationOption="QuasiStatic"
      logLevel="1"
      discretization="FE1"
      targetRegions="{ Domain, Fracture }"
      contactRelationName="fractureContact"
      contactPenaltyStiffness="1.0e0">
      <NonlinearSolverParameters
        newtonTol="1.0e-6"/>
      <LinearSolverParameters
        solverType="gmres"
        krylovTol="1.0e-10"/>
    </SolidMechanicsLagrangianSSLE>

The single-phase fluid flow inside the fracture is solved by the finite volume method in the solver SinglePhaseFVM.

    <SinglePhaseFVM
      name="SinglePhaseFlow"
      logLevel="1"
      discretization="singlePhaseTPFA"
      targetRegions="{ Fracture }">
      <NonlinearSolverParameters
        newtonTol="1.0e-5"
        newtonMaxIter="10"/>
      <LinearSolverParameters
        solverType="gmres"
        krylovTol="1.0e-12"/>
    </SinglePhaseFVM>

The solver SurfaceGenerator defines the fracture region and rock toughness rockToughness="0.3e6". With nodeBasedSIF="1", a node-based Stress Intensity Factor (SIF) calculation is chosen for the fracture propagation criterion.

    <SurfaceGenerator
      name="SurfaceGen"
      targetRegions="{ Domain }"
      nodeBasedSIF="1"      
      rockToughness="0.3e6"
      mpiCommOrder="1"/>

Constitutive laws

For this problem, a homogeneous and isotropic domain with one solid material is assumed. Its mechanical properties and associated fluid rheology are specified in the Constitutive section. The ElasticIsotropic model is used to describe the mechanical behavior of rock when subjected to fluid injection. The single-phase fluid model CompressibleSinglePhaseFluid is selected to simulate the response of water upon fracture propagation.

  <Constitutive>
    <CompressibleSinglePhaseFluid
      name="water"
      defaultDensity="1000"
      defaultViscosity="0.001"
      referencePressure="0.0"
      compressibility="5e-12"
      referenceViscosity="1.0e-3"
      viscosibility="0.0"/>

    <ElasticIsotropic
      name="rock"
      defaultDensity="2700"
      defaultBulkModulus="20.0e9"
      defaultShearModulus="12.0e9"/>

    <CompressibleSolidParallelPlatesPermeability
      name="fractureFilling"
      solidModelName="nullSolid"
      porosityModelName="fracturePorosity"
      permeabilityModelName="fracturePerm"/>

    <NullModel
      name="nullSolid"/>

    <PressurePorosity
      name="fracturePorosity"
      defaultReferencePorosity="1.00"
      referencePressure="0.0"
      compressibility="0.0"/>

    <ParallelPlatesPermeability
      name="fracturePerm"/>

    <FrictionlessContact
      name="fractureContact"/>

    <HydraulicApertureTable
      name="hApertureModel"
      apertureTableName="apertureTable"/>  
  </Constitutive>

All constitutive parameters such as density, viscosity, bulk modulus, and shear modulus are specified in the International System of Units.

Time history function

In the Tasks section, PackCollection tasks are defined to collect time history information from fields. Either the entire field or specified named sets of indices in the field can be collected. In this example, pressureCollection, apertureCollection, hydraulicApertureCollection and areaCollection are specified to output the time history of fracture characterisctics (pressure, width and area). objectPath="ElementRegions/Fracture/FractureSubRegion" indicates that these PackCollection tasks are applied to the fracure element subregion.

  <Tasks>
    <PackCollection
      name="pressureCollection"
      objectPath="ElementRegions/Fracture/FractureSubRegion"
      fieldName="pressure"/>

    <PackCollection
      name="apertureCollection"
      objectPath="ElementRegions/Fracture/FractureSubRegion"
      fieldName="elementAperture"/> 

    <PackCollection
      name="hydraulicApertureCollection"
      objectPath="ElementRegions/Fracture/FractureSubRegion"
      fieldName="hydraulicAperture"/>  

    <PackCollection
      name="areaCollection"
      objectPath="ElementRegions/Fracture/FractureSubRegion"
      fieldName="elementArea"/>

    <!-- Collect aperture, pressure at the source for curve checks -->
    <PackCollection
      name="sourcePressureCollection"
      objectPath="ElementRegions/Fracture/FractureSubRegion"
      fieldName="pressure"
      setNames="{ source }"/>

    <PackCollection
      name="sourceHydraulicApertureCollection"
      objectPath="ElementRegions/Fracture/FractureSubRegion"
      fieldName="hydraulicAperture"
      setNames="{ source }"/>
  </Tasks>

These tasks are triggered using the Event manager with a PeriodicEvent defined for the recurring tasks. GEOS writes one file named after the string defined in the filename keyword and formatted as a HDF5 file (pennyShapedViscosityDominated_output.hdf5). This TimeHistory file contains the collected time history information from specified time history collector. This file includes datasets for the simulation time, fluid pressure, element aperture, hydraulic aperture and element area for the propagating hydraulic fracture. A Python script is prepared to read and query any specified subset of the time history data for verification and visualization.

Initial and boundary conditions

Next, we specify initial and boundary conditions:

Initial values: the waterDensity, separableFace and the ruptureState of the propagating fracture have to be initialized,

Boundary conditions: fluid injection rates and the constraints of the outer boundaries have to be set.

In this example, a mass injection rate SourceFlux (scale="-6.625") is applied at the surfaces of the initial fracture. Only one fourth of the total injection rate is defined in this boundary condition because only a quarter of the fracture is modeled (the problem is symmetric). The value given for scale is $Q_0 \rho_f/4$ (not $Q_0 /4$ ). All the outer boundaries are subject to roller constraints. These boundary conditions are set through the FieldSpecifications section.

  <FieldSpecifications>
    <FieldSpecification
      name="waterDensity"
      initialCondition="1"
      setNames="{ fracture }"
      objectPath="ElementRegions"
      fieldName="water_density"
      scale="1000"/>

    <FieldSpecification
      name="separableFace"
      initialCondition="1"
      setNames="{ core }"
      objectPath="faceManager"
      fieldName="isFaceSeparable"
      scale="1"/>

    <FieldSpecification
      name="frac"
      initialCondition="1"
      setNames="{ fracture }"
      objectPath="faceManager"
      fieldName="ruptureState"
      scale="1"/>

    <FieldSpecification
      name="yconstraint"
      objectPath="nodeManager"
      fieldName="totalDisplacement"
      component="1"
      scale="0.0"
      setNames="{ yneg, ypos }"/>

    <FieldSpecification
      name="zconstraint"
      objectPath="nodeManager"
      fieldName="totalDisplacement"
      component="2"
      scale="0.0"
      setNames="{ zneg, zpos }"/>

    <FieldSpecification
      name="xconstraint"
      objectPath="nodeManager"
      fieldName="totalDisplacement"
      component="0"
      scale="0.0"
      setNames="{ xneg, xpos }"/>

    <SourceFlux
      name="sourceTerm"
      objectPath="ElementRegions/Fracture"
      scale="-6.625"
      setNames="{ source }"/>
  </FieldSpecifications>

The parameters used in the simulation are summarized in the following table.

Symbol	Parameter	Unit	Value
$K$	Bulk Modulus	[GPa]	20.0
$G$	Shear Modulus	[GPa]	12.0
$K_{IC}$	Rock Toughness	[MPa.m^1/2]	0.3
$\mu$	Fluid Viscosity	[Pa.s]	1.0x10^-3
$Q_0$	Injection Rate	[m³/s]	0.0265
$t_{inj}$	Injection Time	[s]	400

Inspecting results

The following figure shows the distribution of $\sigma_{zz}$ at $t=400 s$ within the computational domain..

../../../../../../_images/szz1.png — Fig. 33 Simulation result of $\sigma_{zz}$ at $t=400 s$ 

First, by running the query script

python ./hydrofractureQueries.py pennyShapedViscosityDominated

the HDF5 output is postprocessed and temporal evolution of fracture characterisctics (fluid pressure and fracture width at fluid inlet and fracure radius) are saved into a txt file model-results.txt, which can be used for verification and visualization:

[['      time', '  pressure', '  aperture', '    length']]
         2 1.654e+06 0.0006768     8.137
         4 1.297e+06  0.000743     10.59
         6 1.115e+06 0.0007734     12.36
         8 1.005e+06 0.0007918     13.73
        10 9.482e+05 0.0008189     15.14

Note: GEOS python tools geosx_xml_tools should be installed to run the query script (See Python Tools Setup for details).

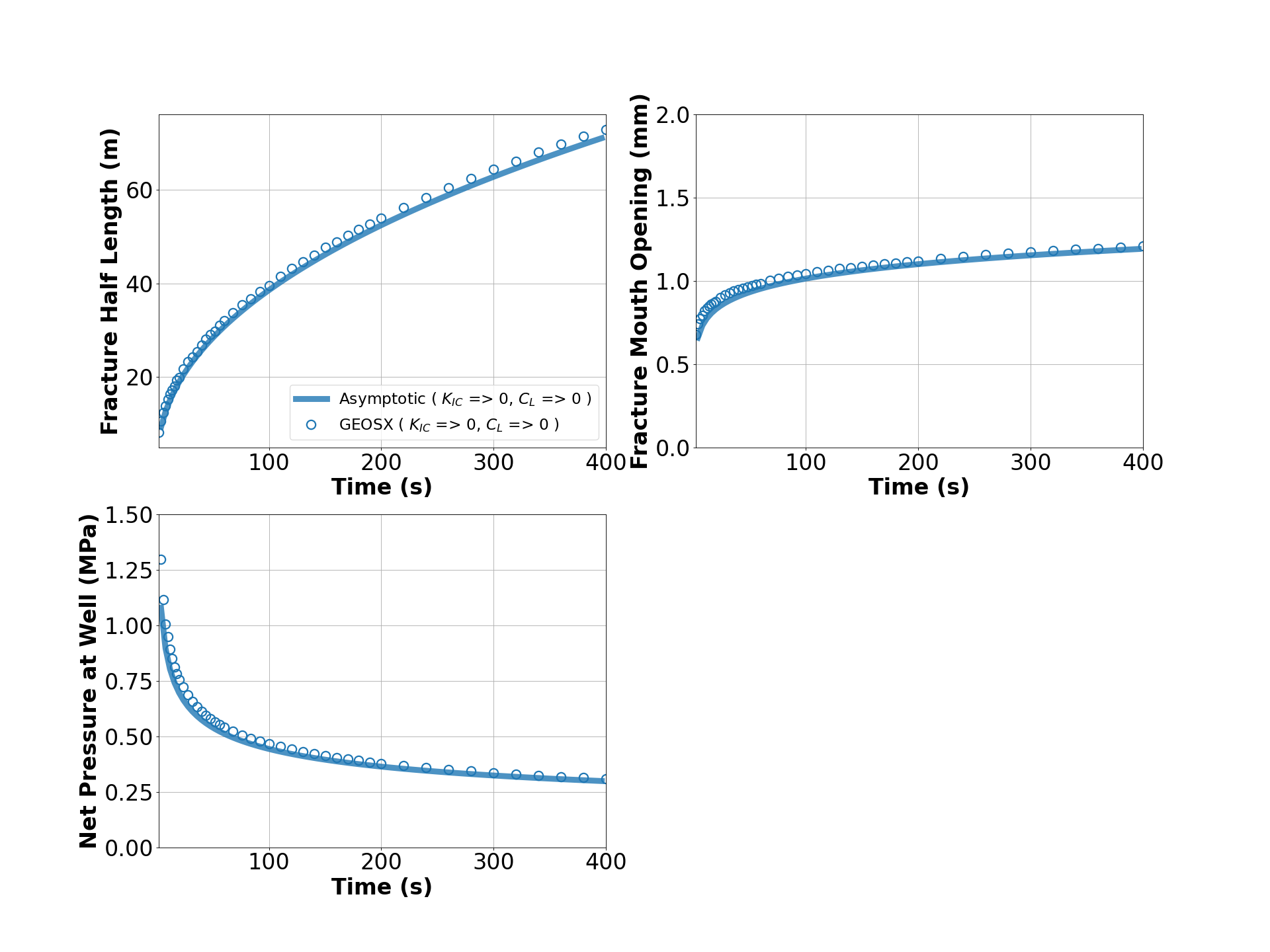
Next, GEOS simulation results (markers) and asymptotic solutions (curves) for the case with viscosity-storage dominated assumptions are plotted together in the following figure, which is generated using the visualization script:

python ./pennyShapedViscosityDominatedFigure.py

As seen, GEOS predictions of the temporal evolution of fracture radius, wellbore aperture and pressure at fluid inlet are nearly identical to the asymptotic solutions.

(Source code)

../../../../../../_images/pennyShapedViscosityDominatedFigure.png

To go further

Feedback on this example

For any feedback on this example, please submit a GitHub issue on the project’s GitHub page.