Deviated Elastic Wellbore Problem

Problem description

This example uses the solid mechanics solver to handle a deviated wellbore problem with open hole completion. This wellbore is subjected to a mud pressure at wellbore wall and undrained condition is assumed (no fluid flow in the rock formation). A segment of the wellbore with isotropic linear elastic deformation is simulated in this case. Far field stresses and gravity effect are excluded. The main goal of this example is to validate the internal wellbore mesh generator and mechanics solver for the case of an inclined wellbore.

Analytical results of the radial and hoop stresses, $\sigma_{rr}$ and $\sigma_{\theta\theta}$ , around the wellbore are expressed as (Detournay and Cheng, 1988) :

$\sigma_{rr} = p_0 \frac{a^2}{r^2}$

$\sigma_{\theta\theta} = -p_0 \frac{a^2}{r^2}$

where $p_0$ is the applied mud pressure at wellbore wall, $a$ is the wellbore radius and $r$ is the radial coordinate.

Input file

This benchmark example uses no external input files and everything required is contained within two GEOS xml files that are located at:

inputFiles/wellbore/DeviatedElasticWellbore_base.xml

and

inputFiles/wellbore/DeviatedElasticWellbore_benchmark.xml

The corresponding xml file for the integrated test is

inputFiles/wellbore/DeviatedElasticWellbore_smoke.xml

In this example, we would focus our attention on the Mesh tag.

Solid mechanics solver

As fluid flow is not considered, only the solid mechanics solver SolidMechanicsLagrangianSSLE is required for solving this wellbore problem.

    <SolidMechanicsLagrangianSSLE
      name="lagsolve"
      timeIntegrationOption="QuasiStatic"
      discretization="FE1"
      logLevel="0"
      targetRegions="{ Omega }"
      >

Deviated wellbore mesh

The internal wellbore mesh generator InternalWellbore is employed to create the mesh of this wellbore problem. The radius of the wellbore and the size of the surrounding rock formation are defined by a vector radius. In the tangent direction, theta angle is specified from 0 to 180 degree for a half of the domain regarding its symmetry. Note that the whole domain could be specified with a theta angle from 0 to 360 degree, if modeling complicated scenarios. The trajectory of the well is defined by trajectory. In this example, the wellbore is inclined in the x-z plane by an angle of 45 degree. The autoSpaceRadialElems parameter allows optimally increasing the element size from local zone around the wellbore to the far-field zone, which is set to 1 to activate this option. The useCartesianOuterBoundary transforms the far-field boundary to a squared shape to enforce a Cartesian aligned outer boundary, which eases the loading of the far-field boundary conditions. In this example, this value is set to 0 for the single region along the radial direction.

  <Mesh>
    <InternalWellbore
      name="mesh1"
      elementTypes="{ C3D8 }"
      radius="{ 0.1, 2 }"
      theta="{ 0, 180 }"
      zCoords="{ -0.5, 0.5 }"
      nr="{ 30 }"
      nt="{ 80 }"
      nz="{ 100 }"
      trajectory="{ { -0.5, 0.0, -0.5 },
                    {  0.5, 0.0,  0.5 } }"
      autoSpaceRadialElems="{ 1 }"
      useCartesianOuterBoundary="0"
      cellBlockNames="{ cb1 }"/>
  </Mesh>

Constitutive law

Isotropic linear elastic constitutive behavior is considered for the rock around the wellbore. Note that the default density is useless in this specific example, as gravity effect is neglected.

    <ElasticIsotropic
      name="shale"
      defaultDensity="2700"
      defaultBulkModulus="5.5556e9"
      defaultShearModulus="4.16667e9"/>

Boundary conditions

Far-field boundaries are subjected to roller constraints and in-situ stresses are not considered. The mud pressure on the wellbore wall is defined by Traction field specification. The nodeset generated by the internal wellbore generator for this face is named as rneg. The traction type is normal to mimic a pressure that is applied normal to the wellbore wall. The negative sign of the scale is attributed to the negative sign convention for compressive stresses in GEOS.

  <FieldSpecifications>

    <FieldSpecification
      name="xConstraint"
      objectPath="nodeManager"
      fieldName="totalDisplacement"
      component="0"
      scale="0.0"
      setNames="{ xneg }"/>

    <FieldSpecification
      name="yConstraint"
      objectPath="nodeManager"
      fieldName="totalDisplacement"
      component="1"
      scale="0.0"
      setNames="{ tneg, tpos }"/>

    <FieldSpecification
      name="zconstraint"
      objectPath="nodeManager"
      fieldName="totalDisplacement"
      component="2"
      scale="0.0"
      setNames="{ zneg }"/>

    <Traction
      name="innerPressure"
      objectPath="faceManager"
      tractionType="normal"
      scale="-10.e6"
      setNames="{ rneg }"/>
  </FieldSpecifications>

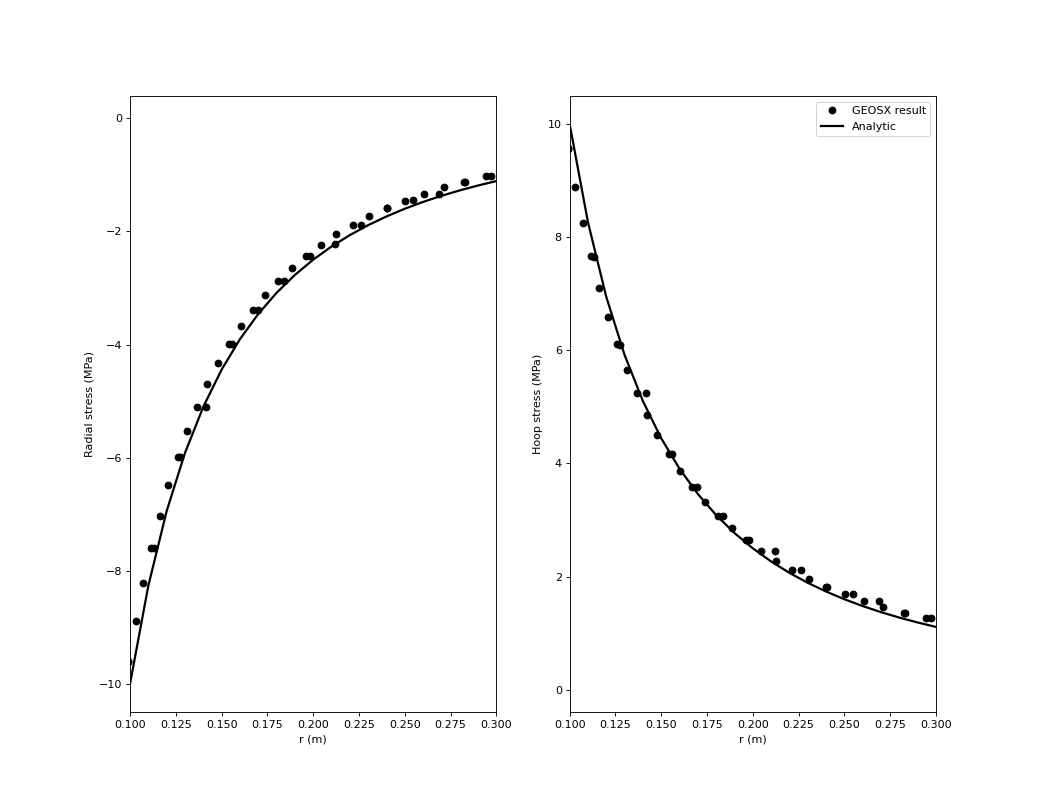
Results and benchmark

A good agreement between the GEOS results and the corresponding analytical solutions is shown in the figure below:

(Source code)

../../../../../../_images/deviatedElasticWellboreFigure.png

To go further

Feedback on this example

This concludes the deviated elastic wellbore example. For any feedback on this example, please submit a GitHub issue on the project’s GitHub page.