Visco Modified CamClay model: Triaxial Driver versus Semi-Analytical Solution

Problem description

This example uses the Triaxial Driver to simulate a visco-elasto-plastic oedometric compression test of a Visco Modified CamClay solid. Oedometric condition with zero lateral strain together with loading/unloading axial strain periods are imposed. Semi-analytical results for the mean and shear stress variations $\Delta p$ and $\Delta q$ can be established, considering the Perzyna approach, for the imposed oedometric boundary conditions as (Runesson et al. 1999) :

$\Delta p = K(\Delta\varepsilon_{V} - \Delta\lambda \frac{\partial G}{\partial p})$

$\Delta q = 2\mu(\Delta\varepsilon_{V} - \Delta\lambda \frac{3}{2}\frac{\partial G}{\partial q})$

where $K$ and $\mu$ are elastic bulk and shear moduli, $G$ is the plastic potential and $\Delta\lambda$ is the visco-plastic multiplier that can be approximated by:

$\Delta\lambda = \frac{\Delta t}{t_*} \frac{F}{3\mu\frac{\partial F}{\partial q}\frac{\partial G}{\partial q} + K\frac{\partial F}{\partial p}\frac{\partial G}{\partial p} + h}$

in which $\Delta t$ is the time increment, $t_*$ is the relaxation time, $F$ is the stress function defining the visco-plastic yield surface and $h$ is the hardening rate defined by:

$h = -\frac{\partial F}{\partial \lambda}$

These solutions are implemented in a Python script associated to this example for verifying GEOS results.

Input files

This validation example uses two GEOS xml files that are located at:

inputFiles/triaxialDriver/triaxialDriver_base.xml

and

inputFiles/triaxialDriver/triaxialDriver_ViscoModifiedCamClay.xml

It also uses a set of table files located at:

inputFiles/triaxialDriver/tables/

A Python script for the semi-analytical solutions presented above as well as for post-processing the GEOS results is provided at:

src/docs/sphinx/advancedExamples/validationStudies/viscoplasticity/ViscoModifiedCamClay/TriaxialDriver_vs_SemiAnalytic_ViscoModifiedCamClay.py

For this example, we focus on the Task and the Constitutive tags.

Task

The imposed axial strain loading/unloading periods, the lateral zero strain, and the initial stress are defined in the Task block as:

  <Tasks>
   <TriaxialDriver
      name="triaxialDriver"
      material="ViscoModifiedCamClay"
      mode="strainControl" 
      axialControl="strainFunction"
      radialControl="zeroStrain"
      initialStress="-1e5"
      steps="200" 
      output="ViscoModifiedCamClayResults.txt" />
  </Tasks>

Constitutive laws

The elasto-visco-plastic parameters are defined as:

    <ViscoModifiedCamClay 
      name="ViscoModifiedCamClay"
      defaultDensity="2700"
      defaultRefPressure="-1e5"
      defaultRefStrainVol="0.0"
      defaultShearModulus="5e7"
      defaultPreConsolidationPressure="-1.5e5"
      defaultCslSlope="1.2"
      defaultRecompressionIndex="0.002"
      defaultVirginCompressionIndex="0.003" 
      relaxationTime="0.1"
    />

All constitutive parameters such as density, viscosity, and the bulk and shear moduli are specified in the International System of Units.

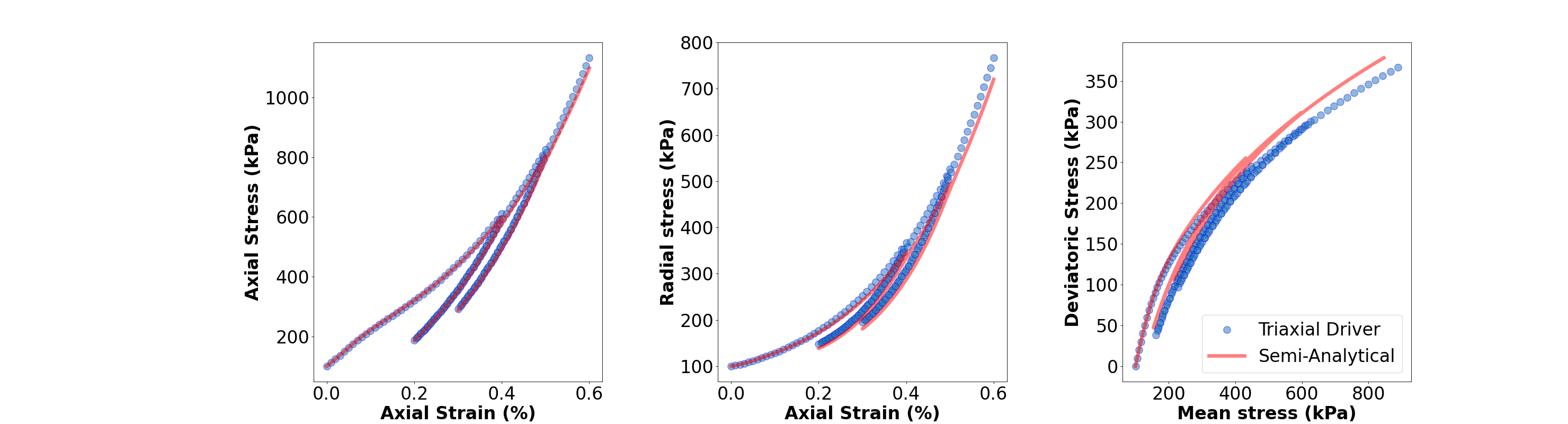
A comparison between GEOS results and semi-analytical results

The simulation results are saved in a text file, named ViscoModifiedCamClayResults.txt. A comparison between the results given by the TriaxialDriver solver in GEOS and the semi-analytical results presented above is shown below. The discrepancy between these results may due to the difference between the Duvaut-Lions approach and the Perzyna approach for time dependant behavior when applying for the Modified CamClay model as discussed by Runesson et al. (1999).

(Source code)

../../../../../../_images/TriaxialDriver_vs_SemiAnalytic_ViscoModifiedCamClay.png

To go further

Feedback on this example

For any feedback on this example, please submit a GitHub issue on the project’s GitHub page.