Model: Modified Cam-Clay

This model may be used to represent a solid material with plastic response to loading according to the Modified Cam-Clay (MCC) critical state model. The MCC yield function is defined as:

$f = q^2 + M^2 p(p - p_c) = 0 ,$

where $p_c$ is the preconsolidation pressure, and $M$ is the slope of the critical state line (CSL). $M$ can be related to the critical state friction angle $\phi_{cs}$ as

$M = \frac{6 \sin \phi_{cs}}{3-\sin \phi_{cs}}.$

Here $f$ represents the yield surface, as shown in Figure 6.

../../../../_images/ModifiedCamClayPQ.png — Fig. 84 Cam-Clay and Modified Cam-Clay yield surfaces in p-q space (Borja, 2013).

Here we use a hyper-elastic constitutive law using the following elastic rate constitutive equation

$\dot{p} = - \frac{p}{c_r} \dot{\epsilon}^e_v,$

where $c_r > 0$ is the elastic compressibility index. The tangential elastic bulk modulus is $K=- \frac{p}{c_r}$ and varies linearly with pressure. We assume a constant shear modulus, and can write stress invariants p and q as

$p = p_0 \exp \left( \frac{\epsilon_{v0} - \epsilon_v^e}{c_r}\right) , \quad q = 3 \mu \epsilon_s^e,$

where $p_0$ is the reference pressure and $\epsilon_{v0}$ is the reference volumetric strain. The hardening law is derived from the linear relationship between logarithm of specific volume and logarithm of preconsolidation pressure, as show in Figure 7.

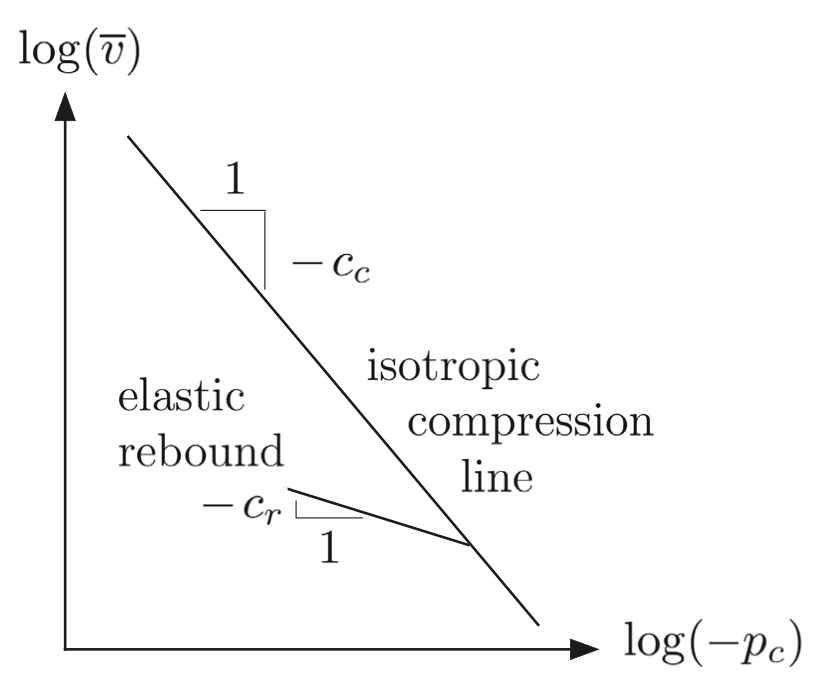
../../../../_images/ModifiedCamClayHardening.png — Fig. 85 Bilogarithmic hardening law derived from isotropic compression tests (Borja, 2013).

The hardening law describes evolution of the preconsolidation pressure $p_c$ as

$\dot{p_c} = - \frac{tr(\dot{\boldsymbol{\epsilon}}^p)}{c_c-c_r} p_c,$

where $c_c$ is the virgin compressibility index and we have $0 < c_r < c_c$ .

Parameters

The supported attributes will be documented soon.

Example

<Constitutive>
  <ModifiedCamClay name="mcc"
                   defaultDensity="2700"
                   defaultRefPressure="-1.0"
                   defaultRefStrainVol="0"
                   defaultShearModulus="200.0"
                   defaultPreConsolidationPressure="-1.5"
                   defaultCslSlope="1.2"
                   defaultRecompressionIndex="0.002"
                   defaultVirginCompressionIndex="0.003" />
</Constitutive>