Modified CamClay Model: Triaxial Driver versus Semi-Analytical Solution

Problem description

This example uses the Triaxial Driver to simulate an elasto-plastic oedometric compression test of a Modified CamClay solid. Oedometric condition with zero lateral strain together with loading/unloading axial strain periods are imposed. Semi-analytical results for the mean and shear stress variations $\Delta p$ and $\Delta q$ can be derived from the imposed vertical strain variation by solving the following equation system:

$\Delta \varepsilon_V = \Delta p(\frac{1}{K} + \frac{1}{h}\frac{\partial F}{\partial p}\frac{\partial G}{\partial p}) + \Delta q \frac{1}{h}\frac{\partial F}{\partial q}\frac{\partial G}{\partial p}$

$\Delta \varepsilon_V = \Delta p \frac{3}{2h}\frac{\partial F}{\partial p}\frac{\partial G}{\partial q} + \Delta q(\frac{1}{2\mu} + \frac{1}{h}\frac{\partial F}{\partial q}\frac{\partial G}{\partial q})$

where $K$ and $\mu$ are elastic bulk and shear moduli, $F$ and $G$ are the plastic yield surface and the plastic potential, and $h$ the is hardening rate defined by:

$h = -\frac{\partial F}{\partial \varepsilon^{vp}_{vol}}\frac{\partial G}{\partial p}$

in which $\varepsilon^{vp}_{vol}$ is the volumetric visco-plastic strain. These solutions are implemented in a Python script associated to this example for verifying GEOS results.

Input files

This validation example uses two GEOS xml files that are located at:

inputFiles/triaxialDriver/triaxialDriver_base.xml

and

inputFiles/triaxialDriver/triaxialDriver_ModifiedCamClay.xml

It also uses a set of table files located at:

inputFiles/triaxialDriver/tables/

A Python script for the semi-analytical solutions presented above as well as for post-processing the GEOS results is provided at:

src/docs/sphinx/advancedExamples/validationStudies/viscoplasticity/ModifiedCamClay/TriaxialDriver_vs_SemiAnalytic_ModifiedCamClay.py

For this example, we focus on the Task and the Constitutive tags.

Task

The imposed axial strain loading/unloading periods, the zero lateral strain as well as the initial stress are defined in the Task block as

  <Tasks>
   <TriaxialDriver
      name="triaxialDriver"
      material="ModifiedCamClay"
      mode="strainControl" 
      axialControl="strainFunction"
      radialControl="zeroStrain"
      initialStress="-1e5"
      steps="200" 
      output="ModifiedCamClayResults.txt" />
  </Tasks>

Constitutive laws

The elasto-plastic parameters are defined as

    <ModifiedCamClay 
      name="ModifiedCamClay"
      defaultDensity="2700"
      defaultRefPressure="-1e5"
      defaultRefStrainVol="0.0"
      defaultShearModulus="5e7"
      defaultPreConsolidationPressure="-1.5e5"
      defaultCslSlope="1.2"
      defaultRecompressionIndex="0.002"
      defaultVirginCompressionIndex="0.003" 
    />

All constitutive parameters such as density, viscosity, bulk and shear moduli are specified in the International System of Units.

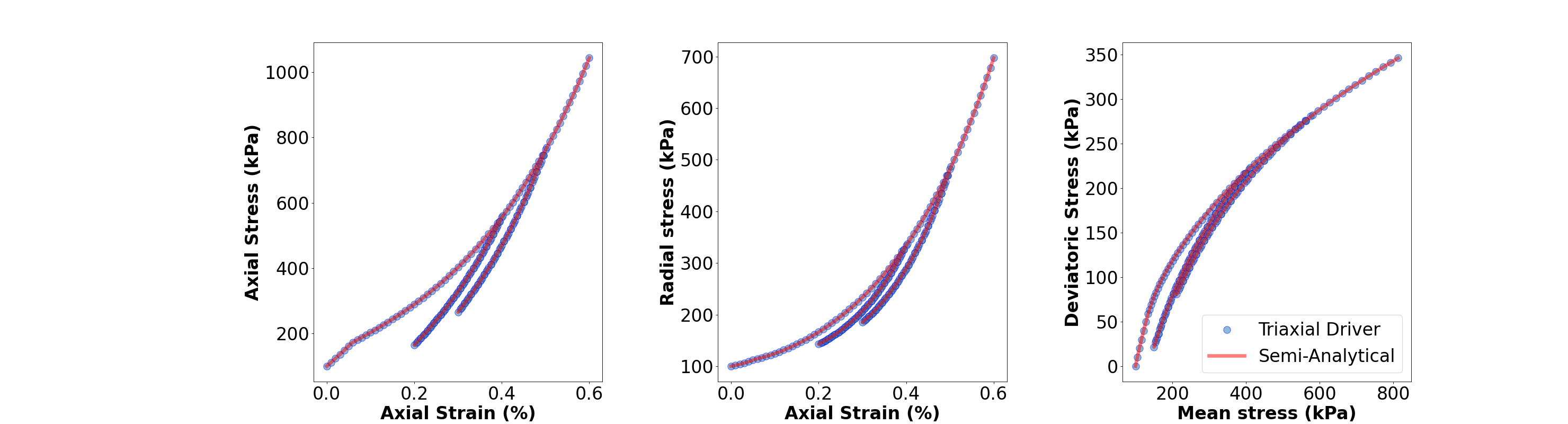
A comparison between GEOS results and semi-analytical results

The simulation results are saved in a text file, named ModifiedCamClayResults.txt. A perfect comparison between the results given by the TriaxialDriver solver in GEOS and the semi-analytical results presented above is shown below:

(Source code)

../../../../../../_images/TriaxialDriver_vs_SemiAnalytic_ModifiedCamClay.png

To go further

Feedback on this example

For any feedback on this example, please submit a GitHub issue on the project’s GitHub page.