Tutorial 2: External Meshes
Context
In this tutorial, we use a simple single-phase flow solver (see Singlephase Flow Solver) to solve for pressure propagation on a mesh that is imported into GEOS. The main goal of this tutorial is to learn how to work with external meshes, and to learn how easy it is to swap meshes on the same physical problem in GEOS. This makes GEOS a powerful tool to solve real field applications with complex geometries and perform assessments of mesh geometry and resolution effects.
Objectives
At the end of this tutorial you will know:
the syntax and format of input meshes,
how to input external files into a GEOS input XML file,
how to run the same physical problem with two different meshes,
how to use and visualize hexahedral and tetrahedral meshes.
Input Files
This tutorial uses an XML file containing the main input for GEOS
and a separate file with all the mesh information.
As we will see later, the main XML file points to the external
mesh file with an include statement.
The XML input file for this test case is located at:
inputFiles/singlePhaseFlow/vtk/3D_10x10x10_compressible_hex_gravity_smoke.xml
The mesh file format used in this tutorial is vtk.
This format is a standard scientific meshing format not specific to GEOS.
vtk is a multi-purpose mesh format (structured, unstructured, serial, parallel, multi-block…) and contains a
compact and complete representation of the mesh geometry and of its properties.
The mesh file used here is human-readable ASCII, and there is a binary storage as well.
It contains a list of nodes with their (x,y,z) coordinates,
and a list of elements that are constructed from these nodes.
Hexahedral elements
In the first part of the tutorial, we will run flow simulations on a mesh made of hexahedral elements. These types of elements are used in classical cartesian grids (sugar cubes) or corner-point grids or pillar grids.
Brief discussion about hexahedral meshes in GEOS
Although closely related, the hexahedral grids that GEOS can process are slightly different than either structured grid or corner-point grids. The differences are worth pointing out here. In GEOS:
Hexahedra can have irregular shapes: no pillars are needed and vertices can be anywhere in space. This is useful for grids that turn, fold, or are heavily bent. Hexahedral blocks should nevertheless have 8 distinct vertices that are not coalesced. Some tolerance exists for degeneration to wedges in some solvers (finite element solvers), but it is best to avoid such situations and label elements according to their actual shape. Butterfly cells, flat cells, negative or zero volume cells will cause problems.
The mesh needs to be conformal: in 3D, this means that neighboring grid blocks have to share exactly a complete face. Note that corner-point grids do not have this requirement and neighboring blocks can be offset. When importing grids from commonly-used geomodeling packages, this is an important consideration. This problem is solved by splitting shifted grid blocks to restore conformity. While it may seem convenient to be able to have offset grid blocks at first, the advantages of conformal grids used in GEOS are worth the extra meshing effort: by using conformal grids, GEOS can run finite element and finite volume simulations on the same mesh without problems, going seamlessly from one numerical method to the other. This is key to enabling multiphysics simulation.
There is no assumption of overall structure: GEOS does not need to know a number of block in the X, Y, Z direction (no NX, NY, NZ) and does not assume that the mesh is a full cartesian domain that the interesting parts of the reservoir must be carved out from. Blocks are numbered by indices that assume nothing about spatial positioning and there is no concept of (i,j,k). This approach also implies that no “masks” are needed to remove inactive or dead cells, as often done in cartesian grids to get the actual reservoir contours from a bounding box, and here we only need to specify grid blocks that are active. For performance and flexibility, this lean approach to meshes is important.
Importing an external mesh with VTK
In this first part of the tutorial, we use an hexahedral mesh provided to GEOS.
This hexahedral mesh is strictly identical to the grid used in the first tutorial (Tutorial 1: First Steps), but instead of using
the internal grid generator GEOS, we specify it with spatial node coordinates in vtk format.
To import external grid into GEOS, we did develop a component directly using the vtk library.
So here, our mesh consists of a simple sugar-cube stack of size 10x10x10. We inject fluid from one vertical face of a cube (the face corresponding to x=0), and we let the pressure equilibrate in the closed domain. The displacement is a single-phase, compressible fluid subject to gravity forces, so we expect the pressure to be constant on the injection face, and to be close to hydrostatic on the opposite plane (x=10). We use GEOS to compute the pressure inside each grid block over a period of time of 100 seconds.

To see how to import such a mesh, we inspect the following XML file:
inputFiles/singlePhaseFlow/vtk/3D_10x10x10_compressible_hex_gravity_smoke.xml
In the XML Mesh tag, instead of an InternalMesh tag,
we have a VTKMesh tag.
We see that a file called cube_10x10x10_hex.vtk is
imported using vtk, and this object is instantiated with a user-defined name value.
The file here contains geometric information in vtk format
(it can also contain properties, as we will see in the next tutorial).
<Mesh>
<VTKMesh
name="CubeHex"
file="cube_10x10x10_hex.vtk"/>
</Mesh>
Here is the vtk file :
# vtk DataFile Version 4.2
Cube structured points dataset
ASCII
DATASET STRUCTURED_POINTS
DIMENSIONS 11 11 11
ORIGIN 0.0 0.0 0.0
SPACING 1.0 1.0 1.0
GEOS can run different physical solvers on different regions of the mesh at different times.
Here, to keep things simple, we run one solver (single-phase flow)
on the entire domain throughout the simulation.
To do so, we need to define a region encompassing the entire domain.
We will name it Domain, as refered to in the single-phase flow solver (in its targetRegions),
and list its constitutive models in the materialList, which are water and rock.
Since we have imported a mesh with only one region, we can set cellBlocks to { * }
(we have could also set cellBlocks to { hexahedra } as the mesh has only hexahedral cells).
<ElementRegions>
<CellElementRegion
name="Domain"
cellBlocks="{ hexahedra }"
materialList="{ water, rock }"/>
</ElementRegions>
Note
If you use a name that is not hexahedra or all for this attribute, or if the mesh is
changed and have not-hexahedral cells, GEOS will throw an error at the beginning of the
simulation. See Meshes for more information.
Running GEOS
The command to run GEOS is
path/to/geosx -i ../../../../../inputFiles/singlePhaseFlow/vtk/3D_10x10x10_compressible_hex_gravity_smoke.xml
Note that all paths for files included in the XML file are relative to this XML file, not to the GEOS executable. When running GEOS, console messages will provide indications regarding the status of the simulation.
In our case, the first lines are:
Adding Mesh: VTKMesh, CubeHex
Adding Event: PeriodicEvent, solverApplications
Adding Event: PeriodicEvent, outputs
Adding Event: PeriodicEvent, restarts
Adding Solver of type SinglePhaseFVM, named SinglePhaseFlow
Adding Geometric Object: Box, left
Adding Output: Silo, siloOutput
Adding Output: Restart, restartOutput
Adding Object CellElementRegion named Domain from ObjectManager::Catalog.
This indicates initialization of GEOS.
The mesh preprocessing tool VTKMesh is launched next,
with console messages as follows.
VTKMesh 'CubeHex': reading mesh from /path/to/inputFiles/singlePhaseFlow/vtk/cube_10x10x10_hex.vtk
Generating global Ids from VTK mesh
VTKMesh 'CubeHex': generating GEOS mesh data structure
Number of nodes: 1331
Number of elems: 1000
C3D8: 1000
Load balancing: min avg max
(element/rank): 1000 1000 1000
Notice the specification of the number of nodes (1331), and hexahedra (1000). After the adjacency calculations, GEOS starts the simulation itself. with the time-step increments specified in the XML file.
At the end of your simulation, you should see something like:
Time: 96s, dt:2s, Cycle: 48
Time: 98s, dt:2s, Cycle: 49
Cleaning up events
SinglePhaseFlow, number of time steps: 50
SinglePhaseFlow, number of successful nonlinear iterations: 50
SinglePhaseFlow, number of successful linear iterations: 450
SinglePhaseFlow, number of time step cuts: 0
SinglePhaseFlow, number of discarded nonlinear iterations: 0
SinglePhaseFlow, number of discarded linear iterations: 0
Umpire HOST sum across ranks: 2.6 MB
Umpire HOST rank max: 2.6 MB
total time 3.518s
initialization time 0.132s
run time 3.076s
Process finished with exit code 0
Once this is done, GEOS is finished and we can inspect the outcome.
Visualization of results in VisIt
All results are written in a format compatible with VisIt.
To load the results, point VisIt to the database file written in the Silo output folder.
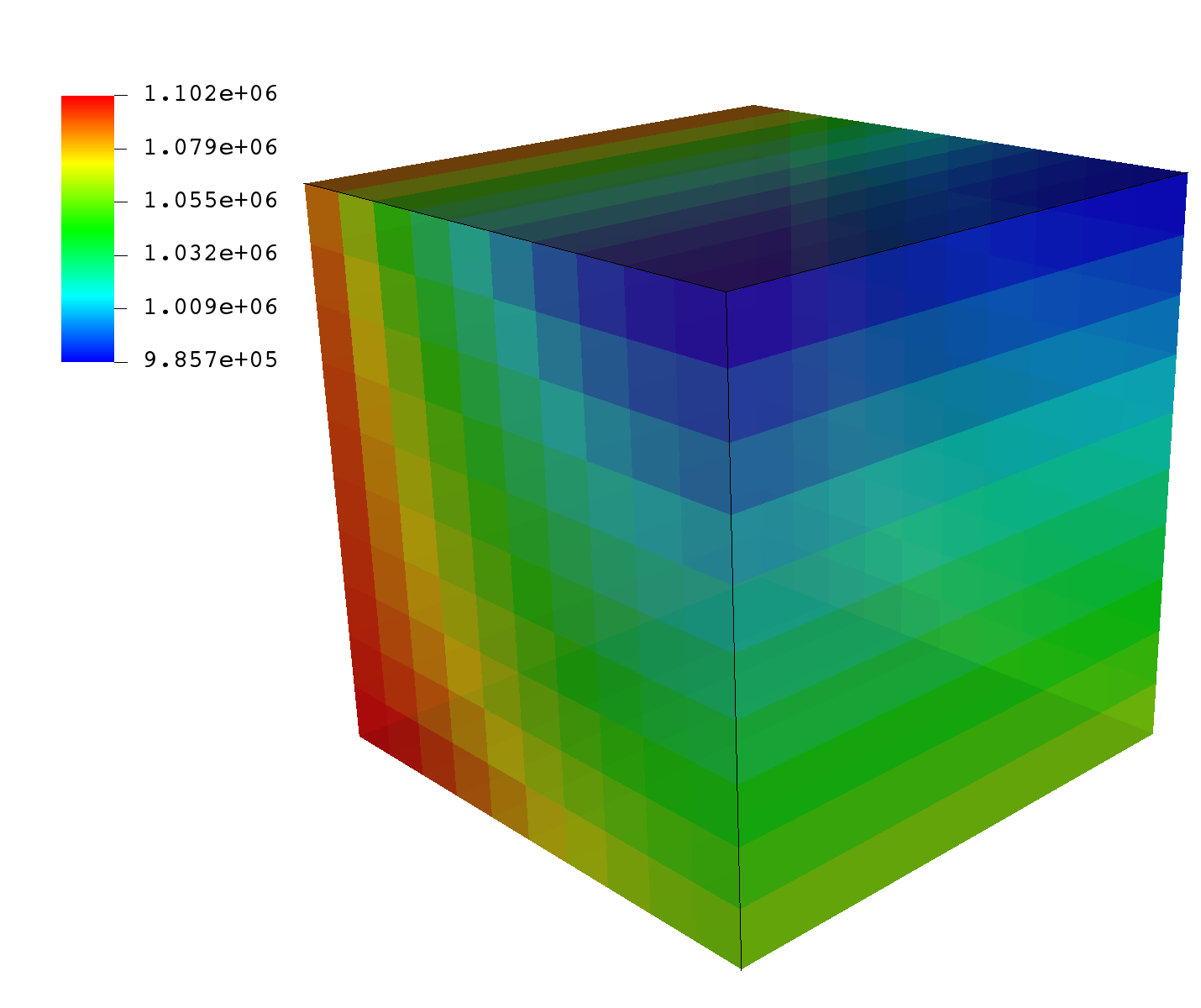
We see that the face x=0 shown here in the back of the illustration applies a constant pressure boundary condition (colored in red), whereas the face across from it displays a pressure field under gravity effect, equilibrated and hydrostatic. These results are consistent with what we expect.
Let us now see if a tetrahedral mesh, under the same exact physical conditions, can reproduce these results.
Externally Generated Tetrahedral Elements
In the second part of the tutorial, we discretize the same cubic domain but with tetrahedral elements. Tetrahedral meshes are not yet common in geomodeling but offer tremendous flexibility in modeling fracture planes, faults, complex reservoir horizons and boundaries. Just like for hexahedral meshes, and for the same reasons (compatibility with finite volume and finite element methods), tetrahedral meshes in GEOS must be conformal.
As stated previously, the problem we wish to solve here is the exact same physical problem as with hexahedral grid blocks. We apply a constant pressure condition (injection) from the x=0 vertical face of the domain, and we let pressure equilibrate over time. We observe the opposite side of the cube and expect to see hydrostatic pressure profiles because of the gravitational effect. The displacement is a single phase, compressible flow subject to gravity forces. We use GEOS to compute the pressure inside each grid block.
The set-up for this problem is almost identical to
the hexahedral mesh set-up. We simply point our Mesh tag to
include a tetrahedral grid. The interest of not relying on I,J,K indices
for any property specification or well trajectory
makes it easy to try different meshes for the same physical problems with GEOS.
Swapping out meshes without requiring other modifications
to the input files makes mesh refinement studies easy to perform with GEOS.
Like before, the XML file for this problem is the following:
inputFiles/singlePhaseFlow/vtk/3D_10x10x10_compressible_tetra_gravity_smoke.xml
The only difference, is that now, the Mesh tag points GEOS to
a different mesh file called cube_10x10x10_tet.vtk.
This file contains nodes and tetrahedral elements in vtk format,
representing a different discretization of the exact same 10x10x10 cubic domain.
<Mesh>
<VTKMesh
name="CubeTetra"
file="cube_10x10x10_tet.vtk"/>
</Mesh>
The mesh now looks like this:

And the vtk file starts as follows (notice the tetrahedral point coordinates as real numbers):
# vtk DataFile Version 2.0
cube
ASCII
DATASET UNSTRUCTURED_GRID
POINTS 366 float
0 0 10
0 0 0
0 10 10
0 10 0
10 0 10
10 0 0
10 10 10
10 10 0
0 0 1.666666666666662
0 0 3.333333333333323
0 0 4.999999999999986
0 0 6.666666666666647
0 0 8.333333333333321
0 1.666666666666662 10
0 3.333333333333323 10
Again, the entire field is one region called Domain which contains water and rock.
Since we have imported a mesh with only one region, we can again set cellBlocks to { * }
(we have could also set cellBlocks to { tetrahedra } as the mesh has only tetrahedric cells).
<ElementRegions>
<CellElementRegion
name="Domain"
cellBlocks="{ tetrahedra }"
materialList="{ water, rock }"/>
</ElementRegions>
Running GEOS
The command to run GEOS is
path/to/geosx -i ../../../../../inputFiles/singlePhaseFlow/vtk/3D_10x10x10_compressible_tetra_gravity_smoke.xml
Again, all paths for files included in the XML file are relative to this XML file, not to the GEOS executable. When running GEOS, console messages will provide indications regarding the status of the simulation. In our case, the first lines are:
Adding Mesh: VTKMesh, CubeTetra
Adding Event: PeriodicEvent, solverApplications
Adding Event: PeriodicEvent, outputs
Adding Event: PeriodicEvent, restarts
Adding Solver of type SinglePhaseFVM, named SinglePhaseFlow
Adding Geometric Object: Box, left
Adding Output: Silo, siloOutput
Adding Output: Restart, restartOutput
Adding Object CellElementRegion named Domain from ObjectManager::Catalog.
Followed by:
VTKMesh 'CubeTetra': reading mesh from /path/to/inputFiles/singlePhaseFlow/vtk/cube_10x10x10_tet.vtk
Generating global Ids from VTK mesh
VTKMesh 'CubeTetra': generating GEOS mesh data structure
Number of nodes: 366
Number of elems: 1153
C3D4: 1153
Load balancing: min avg max
(element/rank): 1153 1153 1153
regionQuadrature: meshBodyName, meshLevelName, regionName, subRegionName = CubeTetra, Level0, Domain, tetrahedra
CubeTetra/Level0/Domain/tetrahedra/water allocated 1 quadrature points
CubeTetra/Level0/Domain/tetrahedra/rock allocated 1 quadrature points
We see that we have now 366 nodes and 1153 tetrahedral elements. And finally, when the simulation is successfully done we see:
Time: 0s, dt:1s, Cycle: 0
Time: 1s, dt:1s, Cycle: 1
Time: 2s, dt:1s, Cycle: 2
Time: 3s, dt:1s, Cycle: 3
Time: 4s, dt:1s, Cycle: 4
Time: 5s, dt:1s, Cycle: 5
...
Time: 95s, dt:1s, Cycle: 95
Time: 96s, dt:1s, Cycle: 96
Time: 97s, dt:1s, Cycle: 97
Time: 98s, dt:1s, Cycle: 98
Time: 99s, dt:1s, Cycle: 99
Cleaning up events
SinglePhaseFlow, number of time steps: 100
SinglePhaseFlow, number of successful nonlinear iterations: 100
SinglePhaseFlow, number of successful linear iterations: 1000
SinglePhaseFlow, number of time step cuts: 0
SinglePhaseFlow, number of discarded nonlinear iterations: 0
SinglePhaseFlow, number of discarded linear iterations: 0
Umpire HOST sum across ranks: 1.9 MB
Umpire HOST rank max: 1.9 MB
total time 5.837s
initialization time 0.094s
run time 5.432s
Process finished with exit code 0
Visualization of results in VisIt
All results are written in a format compatible with VisIt by default. If we load into VisIt the .database file found in the Silo folder, we observe the following results:
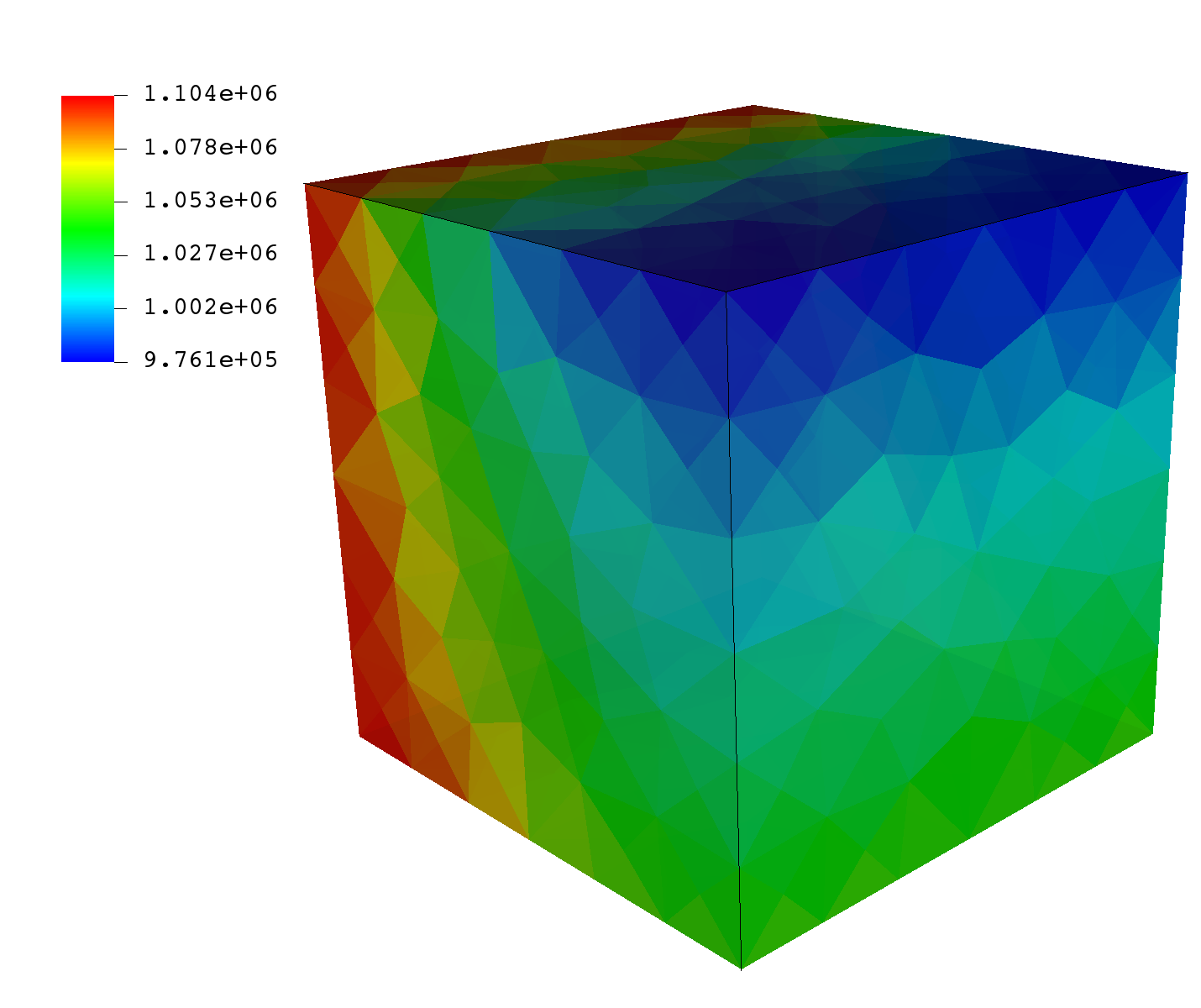
Here, we can see that despite the different mesh sizes and shapes, we are able to recover our pressure profile without any problems, or degradation in runtime performance.
To go further
Feedback on this tutorial
This concludes the single-phase external mesh tutorial. For any feedback on this tutorial, please submit a GitHub issue on the project’s GitHub page.
For more details