Triaxial Driver: Extended Drucker-Prager Elasto-Plastic Model

Context

In this example, we use the TriaxialDriver inside GEOS to simulate rock mechanics experiments, such as triaxial tests. The triaxial driver allows to calibrate properties and model parameters against experimental data before using them in field-scale simulations.

Objectives

At the end of this example, you will know:

how to set up a triaxial test scenario with the TriaxialDriver,

how to define a material model,

how to specify loading conditions with TableFunction,

how to save and postprocess simulation results.

Input file

The XML file for this test case is located at:

inputFiles/triaxialDriver/triaxialDriver_ExtendedDruckerPrager_basicExample.xml

This example also uses a set of table files located at:

inputFiles/triaxialDriver/tables/

Last, a Python script for post-processing the results is provided:

src/docs/sphinx/basicExamples/triaxialDriver/triaxialDriverFigure.py

Description of the case

Instead of launching a full finite-element simulation to mimic experimental loading conditions, GEOS provides a TriaxialDriver to investigate constitutive behaviors and simulate laboratory tests. The triaxial driver makes it easy to interpret the mechanical response and calibrate the constitutive models against experimental data.

In this example, the Extended Drucker-Prager model (see Model: Extended Drucker-Prager) is used to solve elastoplastic deformations of rock samples when subject to controlled loading conditions. The strain-hardening Extended Drucker-Prager model with an associated plastic flow rule is tested in this example. To replicate a typical triaxial test, we use a table function to specify loading conditions in axial and radial directions. The resulting strains and stresses in both directions are numerically calculated and saved into a simple ASCII output file.

For this example, we focus on the Task, the Constitutive, and the Functions tags.

Task

In GEOS, the TriaxialDriver is defined with a dedicated XML structure. The TriaxialDriver is added to a standard XML input deck as a solo task to the Tasks queue and added as a SoloEvent to the event queue.

For this example, we simulate the elastoplastic deformation of a confined specimen caused by external load. A homogeneous domain with one solid material is assumed. The material is named ExtendedDruckerPrager, and its mechanical properties are specified in the Constitutive section.

Different testing modes are available in the TriaxialDriver to mimic different laboratory loading conditions:

mode	axial loading	radial loading	initial stress
`strainControl`	axial strain controlled with `axialControl`	radial strain controlled with `radialControl`	isotropic stress using `initialStress`
`stressControl`	axial stress controlled with `axialControl`	radial stress controlled with `radialControl`	isotropic stress using `initialStress`
`mixedControl`	axial strain controlled with `axialControl`	radial stress controlled with `radialControl`	isotropic stress using `initialStress`

A triaxial test is usually conducted on a confined rock sample to determine material properties. As shown, a conventional triaxial test is described using the mode="mixedControl" testing mode in the TriaxialDriver.

In a triaxial test, the testing sample is under confining pressure (radial stresses) and subject to increased axial load. Therefore, a stress control radialControl="stressFunction" is defined in the radial direction to impose confining pressure. A strain control axialControl="strainFunction" is applied in the axial direction to represent axial compression.

The initial stress is specified by initialStress="-10.e6". To ensure static equilibrium at the first timestep, its value should be consistent with the initial set of applied stresses defined in axial or radial loading functions. This stress has a negative value due to the negative sign convention for compressive stress in GEOS.

Then, steps="200" defines the number of load steps and output="simulationResults.txt" specifies an output file to which the simulation results will be written.

  <Tasks>
    <TriaxialDriver
      name="triaxialDriver"
      material="ExtendedDruckerPrager"
      mode="mixedControl" 
      axialControl="strainFunction"
      radialControl="stressFunction"
      initialStress="-10.e6"
      steps="200" 
      output="simulationResults.txt" />
  </Tasks>

In addition to triaxial tests, volumetric and oedometer tests can be simulated by changing the strainControl mode, and by defining loading controls in axial and radial direction accordingly. A volumetric test can be modelled by setting the axial and radial control functions to the same strain function, whereas an oedometer test runs by setting the radial strain to zero (see Triaxial Driver).

Constitutive laws

Any solid material model implemented in GEOS can be called by the TriaxialDriver.

For this problem, Extended Drucker Prager model ExtendedDruckerPrager is used to describe the mechanical behavior of an isotropic material, when subject to external loading. As for the material parameters, defaultInitialFrictionAngle, defaultResidualFrictionAngle and defaultCohesion denote the initial friction angle, the residual friction angle, and cohesion, respectively, as defined by the Mohr-Coulomb failure envelope. As the residual friction angle defaultResidualFrictionAngle is larger than the initial one defaultInitialFrictionAngle, a strain hardening model is adopted, whose hardening rate is given as defaultHardening="0.0001". If the residual friction angle is set to be less than the initial one, strain weakening will take place. Setting defaultDilationRatio="1.0" corresponds to an associated flow rule.

  <Constitutive>
    <ExtendedDruckerPrager 
      name="ExtendedDruckerPrager"
      defaultDensity="2700"
      defaultBulkModulus="10.0e9"
      defaultShearModulus="6.0e9"
      defaultCohesion="6.0e6"
      defaultInitialFrictionAngle="16.0"
      defaultResidualFrictionAngle="20.0"
      defaultDilationRatio="1.0"
      defaultHardening="0.0001"
    />    
  </Constitutive>

All constitutive parameters such as density, viscosity, bulk modulus, and shear modulus are specified in the International System of Units.

Functions

The TriaxialDriver uses a simple form of time-stepping to advance through the loading steps, allowing for simulating both rate-dependent and rate-independent models.

In this case, users should define two different time history functions (strainFunction and stressFunction) to describe loading conditions in axial and radial direction respectively. More specifically, the table functions in this example include the temporal variations of radial stress and axial strain, which rely upon the external files in the table directory (see Functions). Note that for standard tests with simple loading history, functions can be embedded directly in the XML file without using external tables.

  <Functions>
    <TableFunction
      name="strainFunction"
      inputVarNames="{ time }"
      coordinateFiles="{ tables/time.geos }"
      voxelFile="tables/axialStrain.geos"/>

    <TableFunction
      name="stressFunction"
      inputVarNames="{ time }"
      coordinateFiles="{ tables/time.geos }"
      voxelFile="tables/radialStress.geos"/>
  </Functions>

The strainFunction TableFunction is an example of a 1D interpolated function, which describes the strain as a function of time inputVarNames="{ time }". This table is defined using a single coordinate file:

And a single voxel file:

0.0
-0.004
-0.002
-0.005
-0.003
-0.006

Similarly, the correlation between the confining stress and time is given through the stressFunction defined using the same coordinate file:

And a different voxel file:

-10.0e6
-10.0e6
-10.0e6
-10.0e6
-10.0e6
-10.0e6

For this specific test, the confining stress is kept constant and equal to the initialStress. Instead of monotonic changing the axial load, two loading/unloading cycles are specified in the strainFunction. This way, both plastic loading and elastic unloading can be modeled.

Note that by convention in GEOS, stressFunction and strainFunction have negative values for a compressive test.

Mesh

Even if discretization is not required for the TriaxialDriver, a dummy mesh should be defined to pass all the necessary checks when initializing GEOS and running the module. A dummy mesh should be created in the Mesh section and assigned to the cellBlocks in the ElementRegions section.

  <Mesh>
    <InternalMesh
      name="mesh1"
      elementTypes="{ C3D8 }"
      xCoords="{ 0, 1 }"
      yCoords="{ 0, 1 }"
      zCoords="{ 0, 1 }"
      nx="{ 1 }"
      ny="{ 1 }"
      nz="{ 1 }"
      cellBlockNames="{ cellBlock01 }"/>
  </Mesh>

  <ElementRegions>
    <CellElementRegion
      name="dummy"
      cellBlocks="{ * }"
      materialList="{ dummy }"/>
  </ElementRegions>

Once calibrated, the testing constitutive models can be easily used in full field-scale simulation by adding solver, discretization, and boundary condition blocks to the xml file. Also, it is possible to run a full GEOS model and generate identical results as those provided by the TriaxialDriver.

Running TriaxialDriver

The TriaxialDriver is launched like any other GEOS simulation by using the following command:

path/to/geosx -i triaxialDriver_ExtendedDruckerPrager_basicExample.xml

The running log appears to the console to indicate if the case can be successfully executed or not:

Max threads: 32
MKL max threads: 16
GEOS version 0.2.0 (HEAD, sha1: bb16d72)
Adding Event: SoloEvent, triaxialDriver
   TableFunction: strainFunction
   TableFunction: stressFunction
Adding Mesh: InternalMesh, mesh1
Adding Object CellElementRegion named dummy from ObjectManager::Catalog.
Total number of nodes:8
Total number of elems:1
Rank 0: Total number of nodes:8
        dummy/cellBlock01 does not have a discretization associated with it.
Time: 0s, dt:1s, Cycle: 0
Cleaning up events
Umpire            HOST sum across ranks:   23.2 KB
Umpire            HOST         rank max:   23.2 KB
total time                         0.435s
initialization time                0.053s
run time                           0.004s

Inspecting results

The simulation results are saved in a text file, named simulationResults.txt. This output file has a brief header explaining the meaning of each column. Each row corresponds to one timestep of the driver, starting from initial conditions in the first row.

# column 1 = time
# column 2 = axial_strain
# column 3 = radial_strain_1
# column 4 = radial_strain_2
# column 5 = axial_stress
# column 6 = radial_stress_1
# column 7 = radial_stress_2
# column 8 = newton_iter
# column 9 = residual_norm
0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 -1.0000e+07 -1.0000e+07 -1.0000e+07 0.0000e+00 0.0000e+00
2.5000e-02 -1.0000e-04 2.5000e-05 2.5000e-05 -1.1500e+07 -1.0000e+07 -1.0000e+07 1.0000e+00 0.0000e+00
5.0000e-02 -2.0000e-04 5.0000e-05 5.0000e-05 -1.3000e+07 -1.0000e+07 -1.0000e+07 1.0000e+00 0.0000e+00
7.5000e-02 -3.0000e-04 7.5000e-05 7.5000e-05 -1.4500e+07 -1.0000e+07 -1.0000e+07 1.0000e+00 0.0000e+00
1.0000e-01 -4.0000e-04 1.0000e-04 1.0000e-04 -1.6000e+07 -1.0000e+07 -1.0000e+07 1.0000e+00 0.0000e+00
...

Note that the file contains two columns for radial strains (radial_strain_1 and radial_strain_2) and two columns for radial stresses (radial_stress_1 and radial_stress_2). For isotropic materials, the stresses and strains along the two radial axes would be the same. However, the stresses and strains in the radial directions can differ for cases with anisotropic materials and true-triaxial loading conditions.

This output file can be processed and visualized using any tool. As an example here, with the provided python script, the simulated stress-strain curve, p-q diagram and relationship between volumetric strain and axial strain are plotted, and used to validate results against experimental observations:

(Source code)

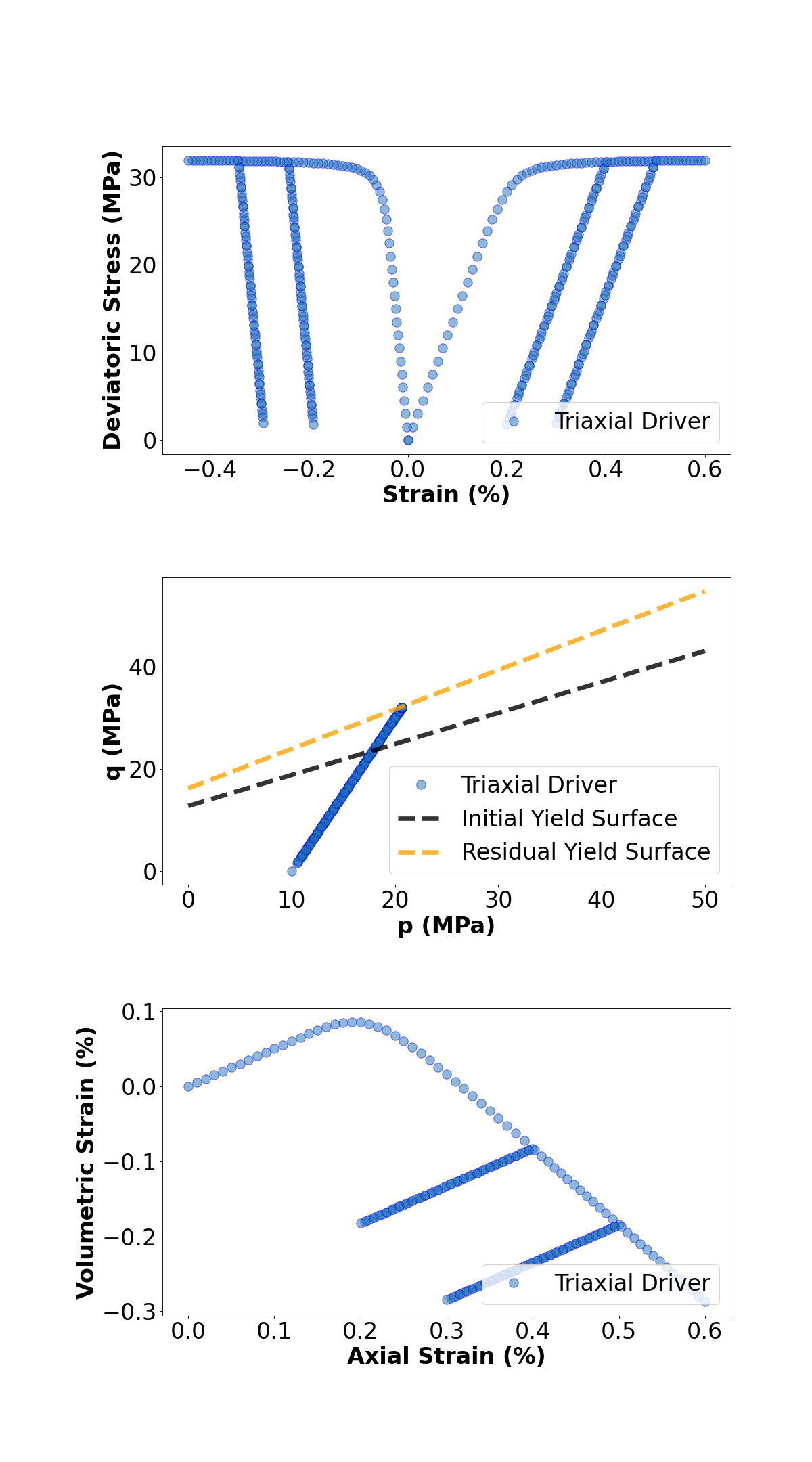
../../../../_images/triaxialDriverFigure.png

To go further

Feedback on this example

For any feedback on this example, please submit a GitHub issue on the project’s GitHub page.