Mesh Hierarchy

In GEOS, the mesh structure consists of a hierarchy of classes intended to encapsulate data and functionality for each topological type. Each class in the mesh hierarchy represents a distinct topological object, such as a nodes, edges, faces, elements, etc. The mesh data structure is illustrated in an object instantiation hierarchy. The object instantiation hierarchy differs from a “class hierarchy” in that it shows how instantiations of each class relate to each other in the data hierarchy rather than how each class type relates to each other in an inheritance diagram.

Fig. 95 Object instances describing the mesh domain. Cardinalities and relationships are indicated.

To illustrate the mesh hierarchy, we propose to present it along with a model with two regions (Top and Bottom) (Fig. 96).

Fig. 96 Example of a model with two regions

DomainPartition

In Fig. 95 the top level object DomainPartition represents a partition of the decomposed physical domain. At this time there is a unique DomainPartition for every MPI rank.

Note

Hypothetically, there may be more than one DomainPartition in cases where the ranks are overloaded. Currently GEOS does not support overloading multiple DomainPartition’s onto a rank, although this may be a future option if its use is properly motivated.

For instance, the model presented as example can be split into two different domains (Fig. 97).

Fig. 97 Mesh partioned in two DomainPartition

MeshBody

The MeshBody represents a topologically distinct mesh body. For instance if a simulation of two separate spheres was required, then one option would be to have both spheres as part of a single mesh body, while another option would be to have each sphere be a individual body.

Note

While not currently utilized in GEOS, the intent is to have the ability to handle the bodies in a multi-body mesh on an individual basis. For instance, when conducting high resolution crush simulations of granular materials (i.e. sand), it may be advantagous to represent each particle as a MeshBody.

MeshLevel

The MeshLevel is intended to facilitate the representation of a multi-level discretization of a MeshBody.

Note

In current practice, the code utilizes a single MeshLevel until such time as we implement a proper multi-level mesh capability. The MeshLevel contains the main components that compose a discretized mesh in GEOS.

Topological Mesh Objects

Each of the “Manager” objects are responsible for holding child objects, data, and providing functionality specific to a single topological object. Each topological object that is used to define a discretized mesh has a “Manager” to allow for simple traversal over the hierarchy, and to provide modular access to data. As such, the NodeManager manages data for the “nodes”, the EdgeManager manages data for the edges, the FaceManager holds data for the faces and the ElementRegionManager manages the physical groups within the MeshLevel ( regions, fractures, wells etc…). Additionally each manager contains index maps to the other types objects that are connected to the objects in that manager. For instance, the FaceManager contains a downward pointing map that gives the nodes that comprise each face in the mesh. Similarly the FaceManager contains an upward pointing map that gives the elements that are connected to a face.

ElementRegionManager

The element data structure is significantly more complicated than the other Managers. While the other managers are “flat” across the MeshLevel, the element data structure seeks to provide a hierarchy in order to define groupings of the physical problem, as well as collecting discretization of similar topology. At the top of the element branch of the hierarchy is the ElementRegionManager. The ElementRegionManager holds a collection of instantiations of ElementRegionBase derived classes.

ElementRegion

Conceptually the ElementRegion are used to defined regions of the problem domain where a PhysicsSolver will be applied.

• The CellElementRegion is related to all the polyhedra

• The FaceElementRegion is related to all the faces that have physical meaning in the domain, such as fractures and faults. This object should not be mistaken with the FaceManager. The FaceManager handles all the faces of the mesh, not only the faces of interest.

• The WellElementRegion is related to the well geometry.

An ElementRegion also has a list of materials allocated at each quadrature point across the entire region. One example of the utility of the ElementRegion is the case of the simulation of the mechanics and flow within subsurface reservoir with an overburden. We could choose to have two ElementRegion, one being the reservoir, and one for the overburden. The mechanics solver would be applied to the entire problem, while the flow problem would be applied only to the reservoir region.

Each ElementRegion holds some number of ElementSubRegion. The ElementSubRegion is meant to hold all the element topologies present in an ElementSubRegion in their own groups. For instance, for a CellElementRegion, there may be one CellElementSubRegion for all tetrahedra, one for all hexahedra, one for all wedges and one for all the pyramids (Fig. 98).

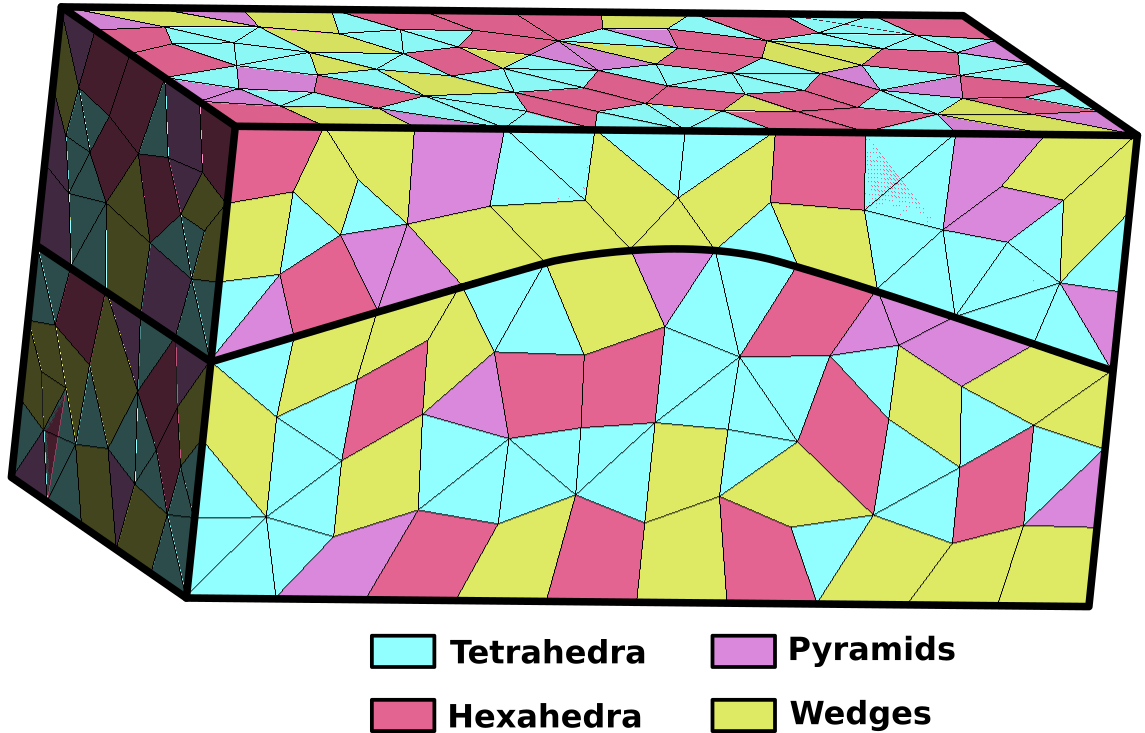
Fig. 98 Model meshed with different cell types

Now that all the classes of the mesh hierarchy has been described, we propose to adapt the diagram presented in Fig. 95 to match with the example presented in Fig. 96.

Direct links to some useful class documentation:

ObjectManagerBase API

MeshLevel API

NodeManager API

FaceManager API